My List of Applied Behavioural Economics Papers to Use in Case Study Assignments

What Do First-Year Economics Students Know About Income Inequality? (Part III)

I've written multiple blogs about my attempts to run interactive classroom exercises, mainly for my first year students, where I get them to guess the level of income inequality. It's part of a longer lecture on inequality and income (re)distribution in general and the idea is that if you want to have a serious discussion about income (re)distribution, you need to have a fairly correct estimate of the existing income inequality.

As blogged previously, I started out using Norton and Ariely's (2011) approach of simply asking what the students thought what percentage of the total income was being earned by various quintiles of the population (ie. what percentage of total income is being earned by the bottom/top 20% of the income distribution?). This consistently leads to students underestimating the income inequality but as Eriksson and Simpson (2011) suggest, this could be caused by an anchoring effect and when I tried their method of instead asking for the average income of the various quintiles, the effect disappeared in my classroom as well.

Although this exercise started out as an attempt to show that students underestimate income inequality, my experience with trying out these activities in the classroom and doing a bit of reading around the topic, is that students don't necessarily underestimate inequality. In fact, they are often surprised by how relatively little you have to earn to be in the top 10% or top 1% earners of the country. Or think that the average UK income is much higher than it really is.

Also, most of the designs of the exercises that are described in the literature and that I have tried out, ask the students to put amounts (or percentages) to different points on the distribution. My thinking is that in the real world we often approach the question from the other direction. We observe an amount – a friend tells us their salary or we see an amount offered in a job advert - and we compare this with other salaries to evaluate if this is relatively high or low; basically, we try and guess where in the income distribution someone earning that particular income might be placed.

Inspired by these two observations I devised a completely new version of the exercise in my Principles of Economics class this year. At the beginning of the segment on income inequality I briefly introduce the exercise as an activity to see what they knew about the income distribution for both the UK (where we are) and the world (where, ehm, we also are). I presented them with a link to the online questionnaire (QR code, I am so modern!) and gave them some background about what I was exactly asking.

I used the data from the World Inequality Database because that was the only source I could find that also included a worldwide measure of income inequality. This database measures income on an individual level but does so by dividing household income by the number of members of the household. Even (young) children have a positive income this way. Also, as far as I can tell they use pre-tax income but do count any pension and unemployment benefits as income.

As you can see above, for the UK I asked the students to guess where in the income distribution we would place someone earning £8.000, £16.000, £24.000, £45.000 and £80.000. For the worldwide comparison I asked slightly different amounts: £1.000, £2.000, £9.000, £24.000 and £45.000. For both the UK and the world I also asked how much an individual would need to earn to be in the top 1% of income distribution (per year, in pounds). Below are the average guesses and the actual numbers.

The results seem to confirm my hypothesis that students actually overestimate income inequality. The estimates for the amounts needed to reach the top 1% are a bit silly because skewed by a couple of extreme outliers but in the other guesses they also almost consistently underestimate the place within the income distribution of various different hypothetical income levels and as such overestimate how much you need to earn to be in the upper reaches of the distribution. This makes for a slightly different discussion compared to the situation where we started with the results of Norton and Ariely's (2011) approach, where students seemed to underestimate inequality.

Ok, so now for the technical bit that is a bit dodgy but bear with me. One way of visualizing the income distribution for a particular country or society is by using a Lorenz curve. Such a graph shows the cumulative population on the horizontal axis and the cumulative share of income on the vertical axis. The graph below shows three examples. You can read off how much the bottom 20% of Norwegians earn and, say, the bottom 60% (about 9% and 38% of the total income). The top 20% earned about 40% of the total. The shape says something about the level of inequality. In particular, the closer the curve is to the 45 degree line, the more equal a society (on the 45 degree line the share of both the bottom and the top 20% will both be 20%). The US and Brazil are more unequal than Norway because the share the bottom 20% and 40% earn is smaller and their Lorenz curve is further from the 45 degree line.

Drawing and interpreting the Lorenz curve is an important part of the lecture on inequality. So it would be nice if I could turn the students’ guesses into a Lorenz curve as an easy (visual) way of comparing their estimations with the actual data. However, because I ask for percentages I don't end up with the neat 20/20/20/20/20 buckets that the standard Lorenz curve assumes.

I figured that I could use the percentages that the students guessed to create my own buckets. It does require a couple of leaps of our imagination. What I did was the following: since my students thought someone earning £8000 was earning more than 17% of the UK population and someone earning £16.000 more than 29%, I took this £8000 as an approximation of what they think the average wage is for someone in the bottom 23% of the population (the halfway point between 17% and 29%). And £16.000 is their approximation of the average earnings of someone between 23% and 35.5% (halfway between 29% and 42%%). At the top end I took their guess of how much you need to earn to be in the top 1% as their approximation of the average earning in the top 10.5% (89.5 being the halfway point between 79% and the upper end of the distribution). Based on these wonky, asymmetric buckets I then calculated the average income share for each of the buckets and used them to draw a Lorenz curve.

Now, this is obviously not the proper way to do economics. For a start, using that estimate for the top 1% (especially if it is as silly as it was in this instance) as the amount for the top 10.5% will sharply overestimate the inequality. On the other hand, if the guesses for the other salaries are all below their actual value, they will actually bring down the total income I am basing my shares on, so that will actually decrease the inequality I calculate using my method. But yes, it’s not ideal but it’s the only way I could do it (I think) and I really really wanted to be able to draw some Lorenz curves.

Below is the one for the UK distribution with the students’ guesses in blue and the actual numbers in orange. Because of my wonky calculation it doesn’t make sense to compare their shape with the ones for Norway (and the US and Brazil) above but I like to think that comparing the students' guesses with the actual numbers side by side like this is still interesting.

The ones for the worldwide income distribution look like this. Again, not really proper Lorenz curves but as way of showing that the students overestimated the income inequality I think they kind of work.

But yeah, despite the problems with drawing the Lorenz curves I am pretty happy with this approach. Will definitely use it again next year. Comments and suggestions for improvement are more than welcome.

What Do First-Year Economics Students Know About Inequality? (Part II)

Not all of my interactive classroom exercises are a success.

A little bit of background: for the last few years I have been using various exercises in my first-year Microeconomics teaching to get students to think about income/wealth inequality. I used to do a version of Norton and Ariely (2011) (it's basically the same as this that went a bit viral last month. I didn't use pie though...). In this exercises students consistently underestimate the income inequality (of the UK in our case) which is a great way of making the topic salient and interesting. However, there are some issues with this particular approach and last year I tried something else which worked a bit too well because the students almost exactly correctly guessed the level of income inequality. Which on the one hand is great but on the other makes it less interesting as a jumping off point to talk about inequality. (I wrote a previous blog about this).

This year I tried the approach described by Kiatpongsan and Norton 2014. They ask their participants to guess a specific type of inequality, the so-called CEO-to-(average)-employee pay ratio and, very promising for my goals, find that people 'dramatically underestimate actual pay inequality'. Dramatically! If that won't make the topic salient I don't know what will. So, feeling optimistic, at the start of the lecture I asked my students to say how much they thought an average CEO of a FTSE 100 earned in a year and what the salary of an avarage UK employee was. (I also asked them what they thought a CEO and an average worker should earn to determine their preferred level of inequality).

According to the CIPD, as reported by the BBC, the average FTSE 100 CEO earned about £3.5million in 2018 and the average full-time worker in the UK earned £29,574 making the CEO earn about 117 times the salary of the average worker. My students were pretty good in guessing the average salary. There was quite some variation (from £20,000 to £52,000) but the average of £29,329 was very close. But they were way off in their guesses of the average earnings of the CEO's. Their average guess was a whopping £43.3million resulting in a CEO-to-employer pay ratio of 1475; about 12 times the actual ratio. Some of this difference is caused by one or two extreme outliers (£870million, really? On average?) but even if you remove these the guessed ratio is at least double the actual one. (Strangely, last year, when I used Eriksson and Simpson (2011)'s method of asking them to guess the average wealth for the bottom 20%, next 20%, middle 20%, next 20% and top 20%, there was quite a lot of variation in absolute numbers but the (average) pay ratio was pretty close to the real one).

So yes, as an exercise to show that actual inequality is larger than the students think, this new approach failed spectacularly. Back to the drawing board. I have some ideas (I think I will go back to Eriksson and Simpson but ask about salaries and not about wealth) but will have to wait until next year to be able to try them out.

First Year Micro-economics Students as Monopolists and Oligopolists

In my first year microeconomics module I have been talking about monopoly and oligopoly markets for the last few weeks. Over the years I have found that one thing my students struggle a bit with in the latter situation is the tension between the cooperative outcome and the competitive (Nash) equilibrium. If I present the situation in a simple pay-off matrix they seem intuitively drawn to the cooperative outcome where the profits are clearly higher than those in the competitive equilibrium. Why would you compete if that is clearly worse for everyone?

To me, this seems like a perfect example of a situation where experiencing the different incentives yourself, instead of observing and thinking about it from the sideline, can help a lot in understanding. Which means that it is a perfect opportunity to do a classroom experiment with the students in the role of a profit maximizing firm.

The set up is quite simple. I divide the class into small groups who all play the role of one firm. They are told they operate in a market where the (inverse) demand for the things they produce can be expressed by the function: Price = 250 - Quantity Supplied. This should be familiar because this is how for the past weeks I have been talking about monopolies and oligopolies: if you want to sell more you have to decrease the price (I only cover the Cournot oligopoly).

The cost side of the story is kept simple: Marginal Cost is constant at 10. There are no Fixed Costs. Each group has a form where they can register their supply decision and keep track of their earnings.

In the first few rounds the firms are the only firm in their market. Everybody is a monopolist. So the firm's profit maximizing supply decision should be quite easy to figure out. Although, to be honest, calculating this using derivatives etcetera isn't part of the learning outcomes of this module; we keep that for the second year. But students should be familiar with MR = MC. A couple of groups do use this method. (The correct answer is a quantity of 120). The rest of the groups take a much easier strategy: try a safe looking number in the first round, observe the profits other groups maker and mimic the highest grossing ones for the next round.

(All decisions and outcomes are public. I use a specially formatted excel-doc to help me calculate the profits and that's projected on the screen in front of the class).

This doesn't go completely right. See above. Supply decisions in the first round are far too cautious (resulting in a high average price but profits below the maximum). But there is considerable overshooting in the other direction in the second round (with some groups proposing a supply of 249). Maybe next year I should do at least one more monopoly round. On paper this version shouldn't be particular interesting because of the lack of strategic element.

In the next stage of the exercise, firms are part of a duopoly market. Every firm has a letter-number code (A1, A2, B1, B2 etc.) and I explain that the two A's interact with each other in market A, the two B's in market B and so forth. The costs and the way the price is determined is the same as before but now the Quantity Supplied in Price = 250 - Quantity Supplied is equal to the total supply by the two firms.

The Nash equilibrium in this duopoly market is where both firms supply 80 units resulting in price of €90. The first thing a lot of groups do, after the rules of the new version are explained, is to look for the group that makes up the other firm in their market to see if there is some deal to be made. In my role as market authority I obviously forbid this kind of attempts at collusive behaviour (but am secretly happy that they know that talking to their competitors might be good for business).

Even without communication the level of competition is not particularly high at first. The average price in the first duopoly period is actually much closer to the cooperative than to the competitive price. (See above. Price in the cooperative situation is obviously the same as in the monopoly situation, €130). Luckily this kind of tacit collusion seems to break down pretty quickly because in the second duopoly period prices are much lower (lower than the competitive equilibrium price even). The third duopoly period I allow for communication between firms within a market. Most firms take advantage of the opportunity. Lots of deals are struck. The majority of which are subsequently broken. But still, the average market price is above the competitive price again.

Whether the students have really understood the point of the exercise - comparing monopoly and duopoly outcome and, especially, why the competitive Nash equilibrium is, well, the equilibrium - we will see in a couple of months in the final test. But their behaviour and decisions and questions made me fairly optimistic.

We did a third version of the game with four firms per market - A1, B1, C1, D1 and A2, B2, C2, D2 - in order to show that more competition leads to even lower prices. And that collusion between 4 firms is more difficult than between two firms. I did find lower average prices in this quatropoly(?) version but not quite as low as the competitive equilibrium predicts. Maybe I should have played this version more than once as well. Prices dropped significantly in the second round of the duopoly too.

Framing and Anchoring (my first year microeconomics students)

In addition to the Endowment Effect I also test my first year microeconomics students for a couple of other classic behavioural economics biases. Since last year I've added a seperate lecture on behavioural economics and I think it helps to make the material more concrete to the students if you can show their own irrational behaviour with a couple of simple exercises.

I must confess that I am not really covering the whole width of behavioural economics in my three non-Endowment Effect exercises because 2 of them are about Framing but they always work and the students usually seem interested in the results. I mean, for the Endowment Effect exercise it takes some effort to explain why WTA and WTP should be similar but in most framing exercises it is pretty clear that we should see the same answers in both conditions.

First of all I do the classic Asian Disease Problem. Which starts:

Imagine that the U.K. is preparing for the outbreak of an unusual disease, which is expected to kill 600 people. Two alternative programs to combat the disease have been proposed. Assume the exact scientific estimate of the consequences of the programs are as follows. Which program would you prefer?

And then there are two versions of the answers:

Program A: 200 people will be saved
Program B: there is a one-third probability that 600 people will be saved, and a two-thirds probability that no people will be saved

and

Program a: 400 people will die
Program b: there is a one-third probability that nobody will die, and a two-third probability that 600 people will die

Students see randomly one of the two versions (AB or ab). Reading them both it should be clear that option A and a are numerically the same and B and b are too but that they are either phrased in terms of saving or losing lives. So yes, you can have a preference for the risky or the certain outcome but it shouldn't matter how it is presented. But it does. The majority of students choose the certain outcome (A) when the problem is presented as saving lives but when the problem is presented in terms of lives lost the vast majority goes for the risky option (b).

The second example is known in the literature as the p-bet and $-bet problem. Here students are presented with the following scenario:

You are offered a ticket in one of the following lotteries:

Lottery A provides a 9/12 chance of winning £110 and a 3/12 chance of losing £10.

Lottery B provides a 3/12 chance of winning £920 and a 9/12 chance of losing £200.

And are asked to answer one of two questions (again randomly determined):

Which one would you prefer? Lottery A or Lottery B

Or:

How much would you be willing to pay for a ticket in lottery A (In pounds)? And in lottery B?

Again, there is no right or wrong answer but the answers should be consistent. Meaning that, if (on average) students prefer lottery A over B then we should also expect students (on average) to be willing to pay more for lottery A than for lottery B. And they don't. When given a choice lottery A is more popular (chosen by 62%) but when asked for how much they are willing to pay for a ticket, the average price for lottery B (£80.00) is higher than the price for A (£33.78).

I don't actually spend a lot of time going over possible reasons for these findings (for the Asian Disease Problem for instance it is related to loss aversion and that we, as humans, are more likely to take risks when something is about losses, or presented as such). I keep that for my third year advanced micro-economics module about behavioural economics but here simply present them as examples of framing: it matters how you present an (economic) question.

The third exercise is supposed to show the Anchoring Effect and is a version of one of Tversky & Kahneman's classic experiments. Each respondent starts with a random number - in my case the last two numbers of their student ID - and they are subsequently asked:

Think of the number above as a percentage. The number of all the countries in Africa that are a member of the United Nations, is that higher or lower than this percentage?

And then:

How many of all the countries in Africa - as a percentage - do you think are a member of the United Nations?

The correct answer to the last question is not really relevant (I have run this experiment for years and I have never bothered looking it up). What's important is that probably not many students know it and, obviously, that the random number the students start with should have no influence on their guess. But in Tversky and Kahneman's case (and many other examples) it does. Respondents who start with a higher random number guess, on average, a higher percentage. The idea is that if irrelevant anchors can have an influence in a question like this, they also might have in other, econonomic, situations. For instance with respect to prices for unfamiliar goods.

The trouble is that I so far have never found this effect in my students. I have been trying this exercise for a number of years but I keep finding no relationship between the random number and the percentage they answer. In previous years I often didn't include the higher/lower question so I blamed that but this year I did it exactly as Tversky and Kahneman did it and I do find a positive relationship, see below, but it's nowhere near statistically significant.

The Endowment Effect (in my first year microeconomics students)

To liven up a pretty dry and technical lecture on the standard model of consumer choice - marginal rate of substition, tangency condition, income and subsitution effect and all that - I run a fairly simple exercise showing the endowment effect in one of the classes of my first year microeconomics module.

Using the online questionnaire tool Qualtrics I ask the students randomly one of two versions of the following question at the start of the lecture:

Imagine you have a bag of winegums (with approx. 100 winegums) and your friend has a Twix. How many winegums would you be willing to give to your friend to get one of his/her Twix bars in return?

or

Imagine you have a Twix and your friend has a bag of winegums (with approx. 100 winegums). How many winegums would your friend have to give to you for you to want to give him/her one of your Twix bars in return?

So what I'm doing is asking for the Willingness to Pay (WTP) and Willingness to Accept (WTA) of one Twix bar expressed in number winegums. Over the course of the lecture I explain about the marginal rate of substitution and how theoretically we would expect the WTA and the WTP of a particular good, for instance Twixes, in terms of the other good, say winegums, to be pretty much the same.

I include some comments at the end about to what extent the model accurately describes how regular people make actual consumption decisions and point out that some of the assumptions, in particular the one about the WTP and WTA being the same for one, are falsified by behaviour in the real world. Pointing out their own valuations for the Twix when exchanging it for winegums, or the other way around. This year again, the WTA was higher than the WTP and I use that for a quick discussion of the endowment effect.

It took me a couple of years of trying to find the right way to ask this question. And still this year there were some issues. There were a couple of responses explaining extreme valuations because winegums are haram or non vegetarian. There were even some students who didn't know what winegums were. But, as I explained to the students a couple of weeks ago when I talked about the recent Nobel Prize in Economics for RCTs (in development economics), if you randomly assign participants to the different treatments and you have enough observations, these kind of issues should average out. But still, maybe next year I will specify that these hypothetical winegums are vegetarian, despite the name don't contain any alcohol and include a picture.

Market Fairness (according to my students)

In my first-year Principles of Micro-economics class I like to use one of Kahneman, Knetsch, and Thaler (1986)'s classic exercises on fairness in markets. I simply ask my students if this:

A hardware store has been selling snow shovels for €15. The morning after a large snowstorm, the store raises the price to €20.

is fair or unfair. The standard economic argument is that it is fair because the increase in price will make sure that all the snow shovels are allocated efficiently. In the real world regular people don't necessarily see it that way. In Kahneman et al.'s study 82% of the respondents think the price increase is unfair.

In my experience my students think much more like economists. Which is not entirely surprising since they are economics students (albeit at the very start of their education). In previous years I asked the question with a simple show of hands and usually the vast majority thought the change in price was fair. This year I used an online questionnaire tool ánd I asked a little earlier (after they had learned about demand and supply and the market equilibrium but before any explicit coverage of efficiency etcetera) and still 52% of the students thought it the action was unfair.

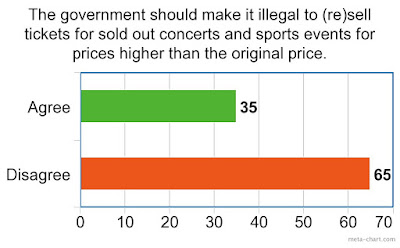
Although I should be content that a considerable number of my students already seem to think like economists in the third week of their degree I do use the results also as an introduction to discuss Richard Thaler's arguments against price gouging.

Using the online questionnaire tool made it easy to ask some other questions on the topic of market outcomes and fairness as well. I framed these two extra questions a bit differently and asked explicitly whether they thought the government should intervene in a particular market. The results suggest that personal experience influences their answers. The majority of the students (who live in London, mostly still with their parents because they can't afford to move out) are in favour of rent control:

On the other hand an almost similar sized majority was against making ticket touts illegal (maybe I should check to what extent individual respondents gave opposite answers to these two questions):